Função Polinomial do 2° Grau ou Função Quadrática

Toda função f: R→R a forma f(x) = ax^2+bx+c , com a diferente de 0 com b e c pertencendo ao conjunto dos  reais é denominada função quadrática, ou função polinomial do 2° grau.

Exemplo

a) F(x)=3x^2+x+1

Representação Gráfica de uma Função Quadrática

Devido ao fato de o gráfico de uma função polinomial do 2° grau ser uma parábola e não uma reta, montaremos o seu gráfico não apenas com dois pares ordenados pertencentes à curva da função e sim com vários, no caso da função quadrática precisamos de mais alguns pontos para termos uma boa idéia de como ficará a curva no gráfico.

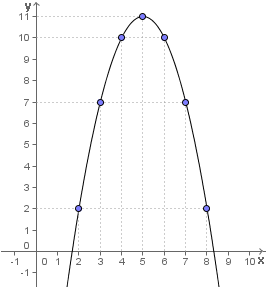
x	y = -x2 + 10x - 14
2	y = -22 + 10 . 2 - 14 = 2
3	y = -32 + 10 . 3 - 14 = 7
4	y = -42 + 10 . 4 - 14 = 10
5	y = -52 + 10 . 5 - 14 = 11
6	y = -62 + 10 . 6 - 14 = 10
7	y = -72 + 10 . 7 - 14 = 7
8	y = -82 + 10 . 8 - 14 = 2

 

Ponto de Intersecção da Parábola com o Eixo das Ordenadas

De uma forma geral a parábola sempre intercepta o eixo y no ponto (0, c).

 

Raiz da Função Quadrática

Observe no gráfico anterior que a parábola da função intercepta o eixo das abscissas em dois pontos. Estes pontos são denominados raiz da função ou zero da função. Uma função quadrática possui quando

∆>0 duas raízes reais distintas

∆<0 nenhuma raiz real

∆=0 uma raiz

 

 

 

 

Coordenadas do Vértice da Parábola

A abscissa do vértice x_v é dada pela fórmula:

x_v = -b/2a

y_v = -∆/-4a

Vamos tomar como exemplo novamente a função y = -x² + 10x - 14 e calcularmos as coordenadas do seu vértice para conferirmos com o ponto indicado na tabela inicial.

Seus coeficientes são:

A=-1; b=10 e c=-14

Então para a abscissa do vértice x_v temos:

x_v = -10/2*(-1) = 5

y_v = -44/-4*(-1)=11